In the previous article in this series, we finished with a parellel SPE-based fractal renderer. This article will cover some of the major optimisations we can do to make use of the Cell Broadband Engine.
Our last benchmark gave us the following results:
| SPE threads | Running time (sec) |
|---|---|
| 1 | 40.72 |
| 2 | 20.75 |
| 4 | 10.78 |
| 6 | 7.44 |
| 8 | 5.81 |
SPE vector instructions
The registers on the SPEs are actually 128-bits wide. Rather than using the entire register for one value, most of the SPE instruction set consists of vector instructions.
For example, say we wanted to add 7 to the value in register one, and place
the result in register two. To do this, we'd use the ai ("add
immediate") instruction:
ai r2,r1,7
This instruction operates on the four 32-bit 'slots' of the 128-bit register (4 x 32 = 128) in parallel:
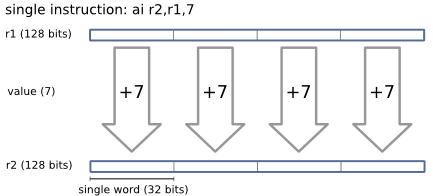
By using these vector instructions, we can do a lot of the fractal rendering work in parallel.
Vector instructions aren't specific to the Cell Broadband Engine - Altivec (on PowerPC processors) and SSE (on Pentium processors) offer similar capabilities for parallel processing of data. In fact, the PPE on the Cell Broadband Engine supports Altivec extensions.
vectorising the fractal renderer
The hackfest task description contains a little information on how to vectorise code:
The SPEs of the Cell/B.E. have an instruction set almost entirely composed of SIMD instructions - so you can do most computations on four operands at a time.
To take advantage of these SIMD capabilities, you can use "vector" types in your code.
For example, consider a simple function to multiply a number by three:
float multiply_by_three(float f) { return f * 3; }
By vectorising this function, we can do four operations in the same amount of time:
vector float multiply_by_three(vector float f); { return f * (vector float){3, 3, 3, 3}; }
The vector float type is similar to an array of 4
floats, except that we can operate on the vector as a whole.
If we look at the instructions generated for both the scalar and vector
versions of the multiply_by_three function, they're exactly the same.
The following code shows the compiled assembly of
multiply_by_three(), both vector and scalar versions. The
function argument is in register 3, return value is placed in register 3.
multiply_by_three: ilhu $2,16448 ; load {3, 3, 3, 3} into register 2 fm $3,$3,$2 ; register 3 = (register 3) * (register 2) bi $lr ; return to caller
So, if you're using scalar operations, we get one multiply in three instructions. Using the vector equivalent, we get four multiplies in three instructions.
So, we should look at the hot paths of the current fractal renderer, and try to vectorise where possible.
Currently, this loop of our render_fractal function is
where the SPE is doing most of the work, iterating over each pixel to find
the point where it diverges to infinity:
for (x = 0; x < params->cols; x++) { cr = x_min + x * params->delta; zr = 0; zi = 0; for (i = 0; i < params->i_max; i++) { /* z = z^2 + c */ tmp = zr*zr - zi*zi + cr; zi = 2.0 * zr * zi + ci; zr = tmp; /* if abs(z) > 2.0 */ if (unlikely(zr*zr + zi*zi > 4.0)) break; } colour_map(¶ms->imgbuf[r * params->cols + x], i, params->i_max); }
The renderer will execute the inner loop up to rows *
columns * i times, where i is between
1 and i_max. Seeing as this is the most executed path in our
renderer code, it is a good place to start our vectorisation efforts.
By vectorising, we can perform the contents of the loop on four pixels at a time (rather than just one), enabling us to reduce the number of iterations to around one quarter.
The new vectorised fractal generator is available in fractal.5.tar.gz.
All we have changed here is the SPE-side code (spe-fractal.c).
The most significant change is to the render_fractal()
function, where we have replaced the above loop with:
for (x = 0; x < params->cols; x += 4) { escaped_i = (vector unsigned int){0, 0, 0, 0}; cr = x_min + spu_splats(params->delta * x); zr = (vector float){0, 0, 0, 0}; zi = (vector float){0, 0, 0, 0}; for (i = 0; i < params->i_max; i++) { /* z = z^2 + c */ tmp = zr*zr - zi*zi + cr; zi = (vector float){2.0f, 2.0f, 2.0f, 2.0f} * zr * zi + ci; zr = tmp; /* escaped = abs(z) > 2 */ escaped = spu_cmpgt(zr * zr + zi * zi, limit); /* escaped_i = escaped ? escaped_i : i */ escaped_i = spu_sel(spu_splats(i), escaped_i, escaped); /* if all four words in escaped are non-zero, * we're done */ if (!spu_extract(spu_orx(~escaped), 0)) break; } colour_map(¶ms->imgbuf[r * params->cols + x], escaped_i, params->i_max); }
This new code processes four columns at each iteration, and increments
x by four each time. We set up a vector of pixels (one per column)
at each iteration, and do the divergence tests on a vector at a time.
Most of the actual aritmetic is easy to convert; the standard multiply, add and subtract operators will work just fine with vector types.
However, the if-test to see if the number has diverged is more
complex - since we're dealing with a vector of four pixels, we can't just break
out of the inner loop when one pixel has diverged. Instead, we need to keep
processing until all vector elements to reach the divergence point, and remember
the value of i where this divergence occurs.
Basically, the above code keeps two extra variables: escaped and
escaped_i. escaped is a vector of four flags - if the
nth word of escaped is non-zero, we have detected that
the nth pixel in our vector has diverged to infinity. The
escaped_i is a similar vector of the value of i where
we first detected this divergence, which is used as the 'value' for each point
in the fractal.
We do this with a few SPE intrinsics, which allow us to use some of the lower-level SPE vector functionality:
spu_cmpgt(a,b)
|
compare greater than returns one bits in each word slot in a that is greater than the
corresponding word slot in b.
|
spu_sel(a,b,c)
|
select bits For bit each bit in c: if the bit is zero, return the
corresponding bit from a, otherwise return the corresponding
bit from b.
|
spu_orx(a)
|
or across Logical-or each word in a, and return the result in the
preferred slot (ie, the first word). The remaining three slots
are set to zero.
|
spu_extract(a,n)
|
extract vector element Return a scalar value from the nth element of
vector a
|
spu_splats(a)
|
splat scalar Return a vector consisting of each word equal to a
|
The first three intrinsics will result in just one instruction in the
compiled code. Since slot 0 is the preferred slot (and therefore where the
compiler would normally store a scalar value in a register), the call to
spu_extract(x, 0) will not result in any instructions at all. The
spu_splats instrinsic may require a variable number of
instructions, depending on the value to splat.
More detail on the SPE instrinsics is available in the PPU & SPU C/C++ Language Extension Specification and SPU Instruction Set Architecture documents on the IBM developerWorks Cell Broadband Engine Resource Center.
We also need to change the colour_map function to take
a vector of i values (rather than just a single value), and
calulate the colours of four pixels at a time. For now, we can just do this
one element at a time, using spu_extract, but this could be
improved later.
benchmarking
After vectorising the SPE fractal code, we can benchmark to see how the vectorisation affects run time. The following table shows run times for the new renederer, along with the proportion of time against the previous scalar implementation.
| SPE threads | Running time (sec) | Vector / Scalar |
|---|---|---|
| 1 | 10.70 | 0.262 |
| 2 | 5.72 | 0.372 |
| 4 | 3.29 | 0.305 |
| 6 | 2.46 | 0.330 |
| 8 | 2.06 | 0.354 |
Not too bad! We're doing much better than our original PPE-based renderer, which took 55.7 seconds to render the same fractal.
Ideally, we'd see a constant vector / scalar figure of 0.25, meaning that we're doing four times the amount of work in the same run time. However, there are still a lot of operations that we haven't optimised yet.
More optimisations in the next article!

Is there a part 5? I can't find it.